CS 자료구조 Binary Search Tree(이진 탐색 트리)

이진 탐색 트리(BST)는 각 노드가 최대 두 개의 자식을 가지는 이진 트리의 특수한 형태로, 데이터의 정렬과 효율적인 검색을 목적으로 설계된 자료 구조다. 노드에 저장된 데이터를 기준으로 왼쪽 서브트리와 오른쪽 서브트리가 특정 조건을 만족하도록 설계되어 있다.

 

ㅇ  이진 탐색 트리의 특징

• 왼쪽 서브트리의 모든 노드는 부모 노드보다 작은 값을 가진다.
• 오른쪽 서브트리의 모든 노드는 부모 노드보다 큰 값을 가진다.

 

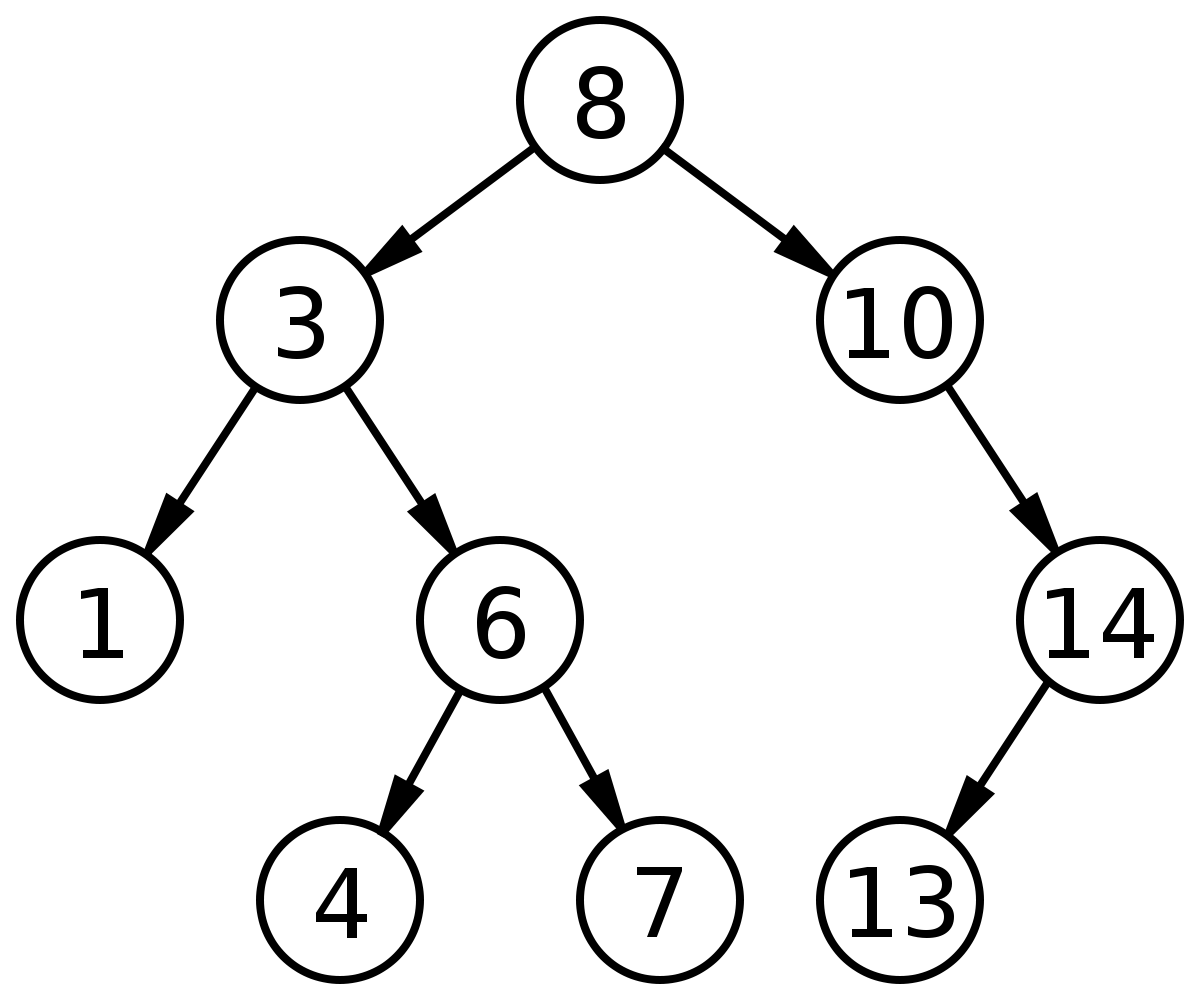
ㅇ 이진 탐색 트리의 주요 연산

탐색(Search)

이진 탐색 트리에서 특정 값을 찾을 때 트리의 루트에서부터 시작한다.

• 찾고자 하는 값이 현재 노드의 값보다 작으면 왼쪽 트리로 이동한다.
• 크면 오른쪽 트리로 이동한다.
• 원하는 값을 찾거나 탐색할 노드가 없으면 종료한다.
• 시간복잡도: 평균적으로 O(log n)이지만 편향 트리의 경우 O(n)이 될 수 있다.

삽입(Insertion)

새로운 값을 삽입할 때도 탐색과 비슷한 방식으로 진행된다.

• 새로 삽입할 값이 현재 노드보다 작으면 왼쪽, 크면 오른쪽으로 이동하며 빈 자리를 찾는다.
• 빈 자리를 발견하면 그 자리에 새 노드를 삽입한다.
• 시간복잡도: 평균 O(log n) 편향일 경우 O(n)이 될 수 있다.

삭제(Deletion)

이진 탐색 트리에서 노드를 삭제하는 경우 세 가지 상황으로 나뉜다.

• 자식이 없는 노드 삭제
  단순히 해당 노드만 제거하면 된다.
• 자식이 하나인 노드 삭제
  자식을 부모 노드에 연결하여 삭제한 노드를 대체한다.
• 자식이 두 개인 노드를 삭제
  삭제된 노드의 자리를 오른쪽 서브트리 최소값 또는 왼쪽 서브트리의 최대 값으로 대체한 뒤 해당 노드를 삭제한다.

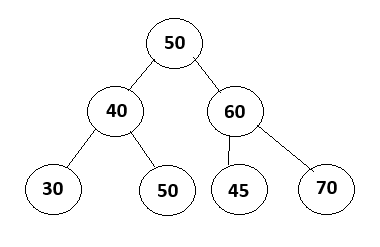
만약 루트 노드인 50을 삭제 한다고 가정하면 왼쪽 서브 트리의 최대 값인 50과 오른쪽 서브트리의 최소 값인 45중에 하나가 루트 노드의 자리를 대체하게 된다. 오른쪽 최소값을 사용하는 것을 더 선호한다.

• 시간 복잡도 : 평균: O(log n) 최악: O(n)

최소값과 최대값 찾기

• 최소값: 왼쪽 자식이 없을 때 까지 왼쪽으로 이동
• 최대값: 오른쪽 자식이 없을 때 까지 오른쪽으로 이동
• 시간 복잡도 : 평균 : O(log n) 최악: O(n)

 

ㅇ 이진 탐색 트리의 장단점

장점

• 빠른 탐색
  평균적으로 이진 탐색 트리는 O(log n)의 시간 복잡도를 가지며, 데이터의 검색 삽입, 삭제 연산에서 빠른 속도를 자랑한다.
• 정렬 유지
  트리 구조 덕분에 데이터를 삽입하는 동시에 정렬된 상태를 유지할 수 있다.

단점

• 편향 트리 문제
  삽입 되는 데이터가 정렬되어 있거나 특정 패턴을 따르는 경우 트리가 한쪽으로 치우치게 되어 O(n)의 시간 복잡도가 발생할 수 있다.
  이 문제를 해결하기 위해 자기 균형 이진 탐색 트리가와 같은 트리들이 고안되었다.

활용 예

• 정렬된 데이터 관리
  데이터의 삽입과 동시에 정렬 상태를 유지하므로, 정렬된 데이터가 필요한 경우 유용하다.
• 데이터 검색
  효울적인 탐색이 가능하여, DB 인덱스, 네트워크 라우팅, 파일 시스템 등에서 자주 사용된다.